Todo Ciencia: Inecuaciones racionales con ejemplos resueltos

Las inecuaciones racionales se presentan con frecuencia en diversos problemas y, en ocasiones, dar con la solución resulta un tanto complicado. Pero con estas sencillas instrucciones ya no habrá dificultad.

El primer paso es identificarlas. Las inecuaciones racionales contienen siempre algún término de la forma:

Siendo P(x) y Q(x) polinomios de cualquier grado.

Las técnicas habituales de resolución de inecuaciones serán útiles a la hora de resolver este tipo de inecuación, siempre que se tenga presente que Q(x) debe ser diferente de 0. De esta manera, cualquier valor que anule el denominador no podrá formar parte de la solución. Esto es lo primero que se debe tener en cuenta a la hora de resolverlas.

Como ejemplos de inecuaciones racionales, se tienen:

Y ahora, una vez identificada la inecuación, y teniendo en mente que cualquier valor que anula el denominador no puede formar parte de la solución, aquí está el segundo punto que debe tenerse en cuenta, y es que para poder resolverla, toda inecuación racional debe llevarse a alguna de las siguientes formas:

Es decir, antes de resolver, hay que convertir toda la inecuación racional en un solo cociente, el cual se compara con 0 de acuerdo al sentido indicado en la desigualdad original. En este aspecto, las desigualdades no se comportan como las ecuaciones, y si queremos aislar la incógnita con las reglas usuales de resolución, se corre el riesgo de no obtener todas las soluciones.

En otras palabras, la desigualdad obtenida podría no ser equivalente a la desigualdad original.

Por ejemplo, es incorrecto hacer lo siguiente:

En su lugar, se hará esto:

Y luego es que se procede a comparar los signos del numerador y del denominador para que se satisfaga la desigualdad planteada.

En el ejemplo propuesto, los valores que anulan el denominador son x = 1 y x= −1, por lo tanto, se tendrá especial cuidado de que no estén incluidos en la solución. La solución completa de esta inecuación se encuentra en el ejemplo 5, al final del post.

Estrategia general para resolver inecuaciones racionales

Paso 1

Si no lo está desde el principio, manipular algebraicamente la inecuación para que resulte un cociente a la izquierda y un cero a la derecha.

Paso 2

Factorizar numerador y denominador, para determinar fácilmente los puntos críticos de la inecuación, que son aquellos en los cuales el numerador y el denominador se hacen cero.

Paso 3

Dividir la recta numérica en intervalos limitados por los puntos críticos hallados en el paso anterior.

Paso 4

En cada intervalo, elegir un valor de prueba y comprobar el signo de la expresión. Anotar el resultado en una tabla o sobre la misma recta numérica.

Paso 5

Seleccionar los intervalos en los que la desigualdad se cumple y anotar cada uno de ellos. Juntos, serán la solución buscada.

Paso 6

Verificar que la solución elegida es correcta, seleccionando algunos valores y sustituyendo en la inecuación original.

Los siguientes ejemplos ilustrarán lo dicho anteriormente.

Ejemplo 1

Resolver la desigualdad racional y expresar la solución como intervalo y en forma gráfica.

Ya la inecuación se presenta de la forma apropiada, es decir, es un cociente a la izquierda y un cero a la derecha. Tampoco es necesario factorizar, puesto que el numerador y el denominador consisten cada uno en un solo factor.

El siguiente paso es determinar los puntos críticos, que anulan respectivamente el numerador y el denominador:

x+2 = 0 ⇨ x=−2

x−1 = 0 ⇨ x=1

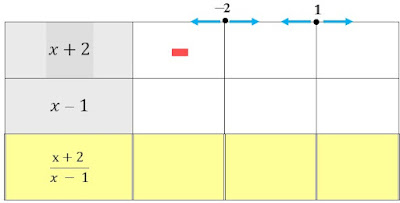
Ahora, con estos puntos, se construye una tabla como la que se muestra a continuación:

En la columna izquierda se tienen los factores que componen la expresión algebraica y en la última fila, la expresión propiamente dicha. Arriba aparecen los puntos críticos que dividen la recta numérica en tres intervalos:

Las flechas azules a la izquierda indican valores menores que el punto crítico, y las flechas que apuntan a la derecha señalan valores mayores.

Lo que sigue es analizar el signo que toma cada factor en cada uno de esos intervalos y colocarlo en la respectiva casilla en blanco. Para ello, se toman valores de prueba arbitrarios.

Análisis del factor x+2

En primer lugar, se analiza lo que sucede con el signo del factor x+2 para valores menores que −2. Por ejemplo, si x = −4, −4+2=−2 es negativo, por lo tanto, se coloca un signo negativo en la casilla correspondiente.

Para valores comprendidos entre −2 y 1, por ejemplo, x= 0, el signo de x+2 es positivo, ya que 0+2=2.

Finalmente, para valores mayores que 1, el factor x+2 es positivo, por ejemplo, para x = 4, 4+2 = 6 es positivo.

Los resultados de los signos para el primer factor quedan así:

Análisis del factor x−1

Para valores menores que −2, el factor x−1 es negativo, por ejemplo, para x = −3, −3−1=−4.

Si se toman valores comprendidos entre −2 y 1, por ejemplo, x = 0, el factor x-1 todavía será negativo: 0−1=−1.

Por último, para valores mayores que 1, por ejemplo 3, el factor x−1 será positivo: 3−1=2.

La tabla de signos hasta el momento es:

El paso final es obtener el signo resultante de la expresión algebraica, usando la bien conocida regla de los signos.

La desigualdad original pide que la expresión racional sea menor que cero, por lo tanto, el intervalo solución es (-2,1).

Y su representación gráfica sobre la recta numérica queda así:

Ejemplo 2

Resolver la desigualdad racional propuesta y expresar la solución como intervalo y en forma gráfica:

Solución

No es necesario factorizar, pero sí es preciso reescribir la inecuación como un cociente único a la izquierda y un cero a la derecha:

Los puntos críticos de la inecuación equivalente resultante son:

Con estos resultados, la tabla de signos queda así:

Interesan los resultados positivos del cociente, ya que este debe ser mayor o igual que 0, por lo tanto, los intervalos seleccionados son el primero y el tercero, de manera que la solución queda establecida así:

Nótese que se utiliza corchete para limitar el primer intervalo, puesto que no hay problema en que x = -5 forme parte de la solución. Pero se emplea un paréntesis para excluir a x=−1, en vista de que este valor anula el denominador, lo que no está permitido. En consecuencia, la solución, en forma gráfica, será:

Ejemplo 3

Resolver la desigualdad racional y expresar la solución como intervalo y en forma gráfica:

Solución

La inecuación ya se presenta factorizada y en la forma apropiada, por lo tanto, se encuentran los ceros de cada factor:

x−3=0 ⇨ x = 3

x+7=0 ⇨ x = −7

(x−5)²= 0 ⇨ x = 5

La tabla tendrá tres factores:

Obsérvese que no siempre los signos de la última fila se alternan, ya que el factor cuadrático siempre es positivo. Los intervalos a seleccionar son aquellos en los que el cociente resulta positivo, y la solución queda establecida como: