Ejercicio 1
Movimiento general en dos dimensiones
 |
| Balón en el aire. Fuente: Dankos-unlmtd a través de Flickr. |
Solución a
Solución b
Solución c
Ejercicio 2
Movimiento de proyectiles (lanzamiento horizontal)
Una esfera rueda horizontalmente con una rapidez de 7.6
m/s y se cae por el borde de una plataforma alta. Si la esfera cae a 8.7 m de
un punto en el suelo que está directamente abajo del borde de la plataforma,
¿qué altura tiene la plataforma?
Solución
Si el origen del sistema de coordenadas se encuentra en el
lugar del lanzamiento, el vector de posición del móvil se puede escribir así:
r (t) = x(t) i + y(t) j
Con:
x(t) = v0x∙t
y(t) = ½ g∙t2
La incógnita a calcular es el valor de ‘y’ mostrado en la figura,
es decir, la altura de la plataforma.
Como en el enunciado se dice que la esfera cae a una
distancia horizontal de x = 8.7 m del pie de la plataforma, si en x(t) se
sustituye este valor, más la velocidad inicial de magnitud vox = 7.6
m/s, se podrá despejar fácilmente el tiempo que dura la caída, también llamado tiempo
de vuelo:
Este resultado se sustituye en la
ecuación de y(t) y con esto se calcula la altura solicitada:
y(t) = ½ g∙t2 = ½ 9.8 m/s2×
(1.14 s)2 = 6.37 m
Ejercicio 3
Movimiento de proyectiles (lanzamiento inclinado)
Solución a
Necesitaremos las componentes de la velocidad inicial:
vox = vo . cos θ = 100 x cos 37º ft/s = 80 ft/s
El vector velocidad es:
v (t) = vx (t) i + vy (t) j
Con:
vy (t) = voy – gt
Se toma el valor de la aceleración de gravedad como g = 32 ft/s2, ya que los datos del problema están en las unidades del sistema británico de medidas:
vy (1) = 60 – (32×1) ft/s = 28 ft/s
El vector buscado es:
v (t) = 80 i + 28 j ft/s
La partícula va de subida, ya que la velocidad en j es positiva.
Solución b
La altura máxima es:
Solución c
Solución d
Ejercicio 4
Movimiento de proyectiles (lanzamiento inclinado)
a) ¿Durante cuánto tiempo está la pelota en el aire?
b) ¿A qué distancia de la base de la casa cae la pelota?
c) ¿Cuál es su rapidez justo antes de que haga contacto con
el suelo?
 |
| Fuente: Física. Wilson, A. |
Solución a
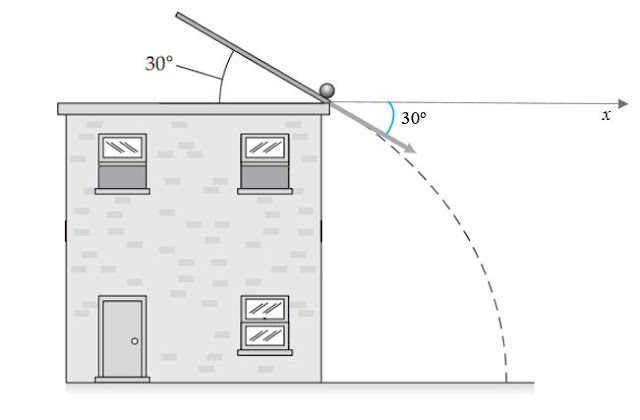
La pelota abandona la azotea con la velocidad inicial
dirigida en el sentido de la flecha, formando un ángulo de 30º por debajo
de la horizontal. Esto quiere decir que el vector velocidad inicial tiene
componente horizontal positiva y componente vertical negativa, por lo tanto:
v0x
= 5 m/s × cos 30º = 4.33 m/s
v0y
= − 5 m/s × sen 30º = − 2.50 m/s
Los resultados se sustituyen en las ecuaciones de posición,
donde se elige xo =; yo=0 en el punto de lanzamiento, al
borde de la azotea, para simplificar las ecuaciones
x(t) = v0x∙t
y(t) = v0y ∙t − ½ g∙t2
El enunciado dice que la distancia vertical entre el punto
donde comienza la caída y el suelo es de 7.00 m. Si el origen se escoge en el
punto de lanzamiento y el sentido hacia abajo es negativo, entonces:
y(t) = −7.00
Tomando g = 9.81 m/s2 para la aceleración de la
gravedad y sustituyendo valores:
y(t) = v0y ∙t − ½ g∙t2 = −2.50
× t
−
½× 9.81×t2
= −2.50t
− 4.91t2
= −7.00
Resulta una ecuación de segundo grado en ‘t’, que se puede
resolver fácilmente:
− 4.91t2 − 2.50t + 7.00 = 0
Las soluciones son:
t1 = −1.48 y t2 = 0.97
Se descarta la primera porque el tiempo no es negativo, por lo que
el tiempo que la pelota tarda en caer los 7.00 m, es decir, el tiempo de vuelo,
es igual a t = 0.97 s.
Solución b
La distancia horizontal a la que llega la pelota, o alcance
máximo horizontal se obtiene sustituyendo el tiempo anterior en:
x(t) = v0x∙t
Por lo tanto:
xmax
= 4.33 m/s × 0.97 s = 4.20 m
Solución c
Para encontrar la rapidez final, primero hay que encontrar las
componentes del vector velocidad final. Como se recordará, la velocidad
horizontal en este movimiento permanece constante, por lo tanto:
v0x = vx = 4.33 m/s
La componente vertical de la velocidad se encuentra de la
ecuación para el movimiento uniformemente acelerado:
vy = v0y – gt
Sustituyendo valores:
vy = v0y – gt
vy
= (−2.50 – 9.81× 0.97) m/s = –12.02 m/s
Tiene sentido que esta componente sea negativa, puesto que está
dirigida hacia abajo.
Ahora se escribe el vector velocidad final:
v = 4.33 i –12.02 j
m/s
Y su modulo o magnitud se calcula mediante:
Ejercicio 5
Movimiento circular
Solución a
Solución b
Solución c
Solución d
Ejercicio 6
Movimiento circular uniforme
Una rueda de 50 cm de radio gira a 180 r.p.m. Calcular:
a) El módulo de la velocidad angular de un punto en su
borde, en rad/s
b) El módulo de la velocidad lineal de un punto en su borde.
c) La frecuencia
Solución a
El módulo de la velocidad angular ‘ω’ ya lo da el enunciado, solo que
está en r.p.m., que son las iniciales de ‘revoluciones por minuto’.
Para convertir a radianes las revoluciones, se tiene en
cuenta que:
1 revolución = 2π radianes
Y para convertir los minutos a segundos:
1 minuto = 60 segundos
Por lo tanto:
Solución b
Las magnitudes de la velocidad angular y la velocidad lineal
están relacionadas mediante:
v = ω.r
Basta con sustituir valores, teniendo en cuenta que r = 50
cm = 0.5 m:
v = 6π rad /s × 0.5 m = 3π m /s
Solución c
Para encontrar la frecuencia se usa:
f = ω / 2π = 6π rad /s ÷ 2π rad = 3 Hz
Ejercicio 7
Movimiento relativo en dos dimensiones
La velocidad de una partícula en el marco de
referencia A es 2.0 i +3.0 j m/s. La
velocidad del marco de referencia A con respecto al marco de referencia B es 4.0 k m/s, y
la velocidad del marco de referencia B con respecto a C es 2.0
j m/s.
¿Cuál es la velocidad de la partícula en el marco de
referencia C?
Solución
Se usará el método de los subíndices, con la siguiente
nomenclatura:
P = partícula; marco de referencia A = A; marco de
referencia B = B; marco de referencia C = C
Las velocidades se denotan de la siguiente manera:
Velocidad de la partícula en el marco de referencia A
Velocidad del marco de referencia B respecto al marco
de referencia C
Enseguida se plantea la suma vectorial:
Obsérvese que:
Ejercicio 8
Movimiento relativo en dos dimensiones
Se sabe que un bote es capaz de moverse a 8,0 km/h en
aguas tranquilas, pero ahora se desplaza sobre un río cuya corriente es de 3,0
km/h con respecto a la orilla.
Con esta información, responder las siguientes preguntas:
a) ¿Cuánto tiempo se necesita para remar 1,5 km aguas abajo?
b) ¿Cuánto tiempo se necesita para el viaje de vuelta?
c) ¿En qué dirección debe apuntar el bote para llegar en
línea recta a la otra orilla del río?
d) Suponiendo que el río tiene 0,8 km de ancho. ¿Cuál es la velocidad del bote con respecto a la orilla y cuánto tiempo se requiere para llegar a la orilla opuesta?
Solución a
Se utilizarán los siguientes subíndices para denotar las velocidades:
T = tierra; B = bote; R = río
Como en este caso, el bote rema en la misma dirección que la
corriente del río, y de acuerdo al sistema de coordenadas mostrado en la figura
de abajo, se tendrá lo siguiente:
Velocidad del bote respecto al río en calma
Velocidad del río respecto a tierra
Importante: ‘tierra’
es equivalente a decir ‘orilla’.
Será necesario hallar la velocidad del bote con respecto a tierra mientras se mueve sobre la corriente:
Nótese que la corriente ayuda al bote a moverse en la dirección
del eje +x, que es la dirección ‘aguas abajo’ señalada por el enunciado, como
se muestra en la figura siguiente:
Teniendo en cuenta esto, los subíndices para la suma
vectorial de las velocidades quedan así:
Por lo tanto:
Puesto que el movimiento es rectilíneo
uniforme, el tiempo que tarda en recorrer d =1.5 km con esta velocidad es:
Solución b
Ahora el bote rema en sentido contrario a la corriente, por
lo tanto, debe tomarle más tiempo regresar, ya que la corriente no lo ayuda.
Gráficamente, esta es la situación:
La velocidad del bote en estas circunstancias es:
Y con esta velocidad, el tiempo que le
toma al bote regresar es:
Solución c
Ahora, nuestro bote desea moverse perpendicularmente al río, pero la corriente no se lo permite. En cuanto el bote se de a la tarea de remar hasta la otra orilla, la corriente lo desviará un ángulo θ, como se observa del siguiente diagrama:
Para evitarlo, el bote tendrá que remar colocando la proa en
el ángulo α mostrado en este diagrama. Nótese que α y θ no tienen necesariamente
el mismo valor:
Solución d
Del triángulo anterior, se puede calcular la rapidez del
bote respecto a tierra, con la corrección de rumbo establecida en el apartado c:
Por lo que el tiempo necesario para
llegar a la orilla opuesta con esta corrección de rumbo es:
No hay comentarios:
Publicar un comentario